Tunnel Vision for Numbers – where is the critical thinking in problem solving?
- lammandys
- Feb 4, 2016
- 3 min read
Updated: Apr 20, 2021

Recently, two problems completed by Grade 3 students caught my attention. So I analyzed the errors my students made.
Jason and his two brothers have to share a pack of 24 cans of pop. But, his older brother already took 12. How many cans of pop does Jason get to share with his younger brother?
A common wrong answer I noticed was 24 divided by 12, to get an answer of 2.
Another common mistake was 24 cans of pop divided by 2 brothers, resulting in the answer of 12 cans.
The correct answer is, of course, 24 cans subtracting 12 cans, and then dividing between 2 people, Jason and his younger brother. The answer is 6 cans per person.
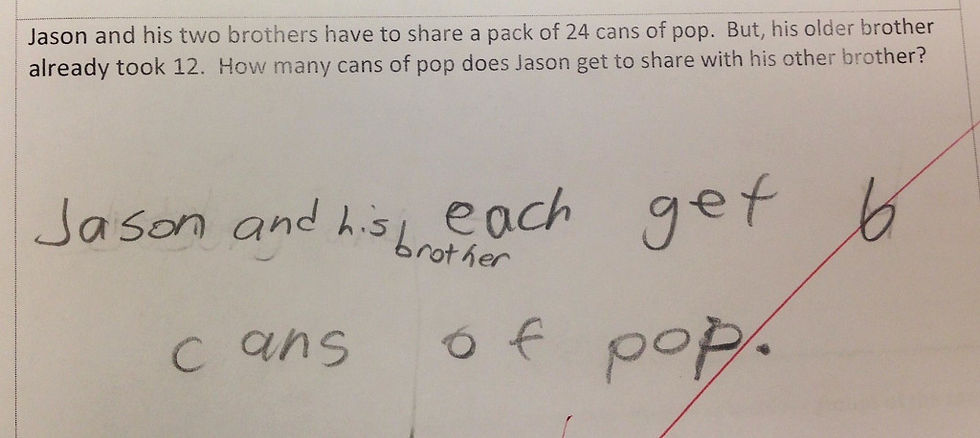
A second problem…
Jamie’s dad bought 24 binders for her and her two brothers. How many binders does each of them get?
Correct answer: 24 binder / (1 person + 2 brothers) = 8 binders
Common incorrect answer: 24 / 2 = 12 binders
Looking at these common errors, I realized that some of the students were having a tunnel vision for numbers. It’s also like apple picking. When the reddest and juiciest apples catch your eyes, pick them from the tree and throw them in your basket. As soon as students see numerical values in a word problem, they just can’t resist picking them off without a closer look. Take a look at the above questions again, the common mistakes are associated with picking the numbers that appear in the question, and then dividing them. Critical thinking was not necessarily used in the students’ process of solving the problem. Unfortunately, this “apple-picking” approach to solving a problem is also quite common in the college math classroom too.
This reminds me of a classic problem:
There are 125 sheep and 5 dogs in a flock. How old is the shepherd?
You might be thinking… “What?!” You might read the above problem again and now ponder the mathematical relationship between the amount of livestock and the age of the shepherd. And you would realize that the problem is nonsensical.
Interestingly, in the 1990’s, the above problem was presented to elementary school students. Three out of four completed the problem with a numerical answer using all sorts of operations.
125 + 5 =130
125 – 5 = 120
125 / 5 = 25
And well, because 25 sounds reasonable to be the age of the shepherd, it was one way for these students to answer the question.
In 2013, Robert Kaplinsky, a mathematics education specialist revisited this. Grade 8 students in the U.S. were put to the test and were asked this classic problem. Similarly, 75% of the students gave a numerical answer. Methods the students took included the three above, but there were also 4 students in a class of 32, who had guessed their answer completely to give a numerical answer.
In a Grade 6 classroom, the results came out worse as 100% of them gave a numerical answer.
What do these results mean?
One simple answer is that students are not prepared adequately to critically solve a problem. Often mathematics is seen as a subject of following a set of rules. In other words, when students come across a problem, rather than making sense of the problem, they apply rules they have learned to numbers that they pick out from the problem.
Teach students to make sense of the problem:
Robert Kaplinsky, the math specialist, suggested that students who make sense of problem should be able to do the following:
Explain the meaning of the problem
Plan a solution pathway instead of attempting to find a solution without reasoning
Question “does this make sense?” throughout the problem, from the point of understanding the problem to figuring out whether the answer makes sense.
I would add one more thing, to help students question “does this make sense”, encourage numerical estimation, encourage pattern building, and encourage them to look at the relationship between the quantities. Get them to ask “what would a wrong answer look like?”
Last but not least, don’t forget that critical thinking is all about: curiosity, flexibility, and keeping an open mind.
Written by Mandy Lam






Comments